[Data Structure] Binary Search Trees
Binary Search Trees
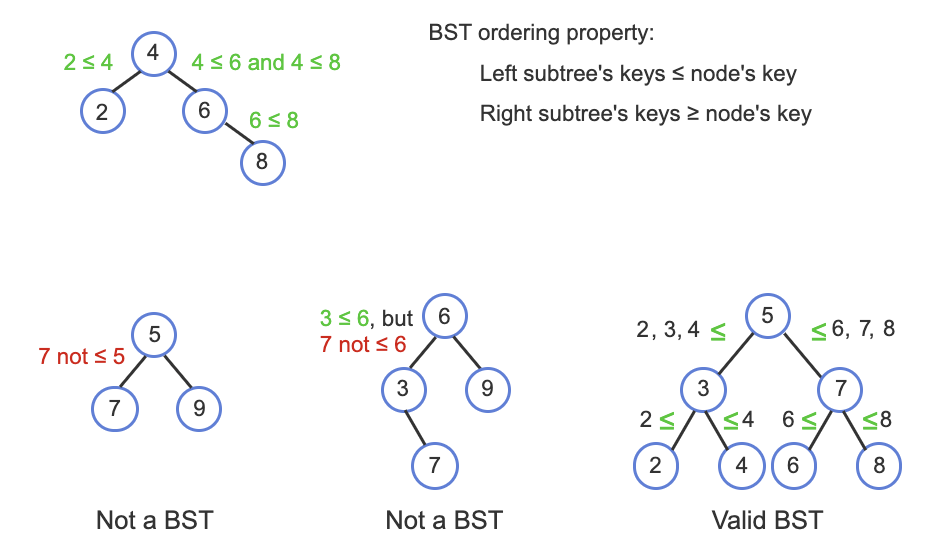
An especially useful form of binary tree is a binary serach tree (BST).
BST has an ordering property that any node's left subtree keys ≤ the node's key and the right subtree's keys ≥ the node's key.
This property enables fast searching for an item.
Searching
To search nodes means to find a node with a desired key, if such a node exists.
A BST may yield faster searches than a list.
Searching a BST starts by visiting the root node.
# Pseudocode for Search
if (currentNode→key == desiredkey):
return currentNode
else if (desiredkey < currentNode→key):
# Visit left child, repeat
else if (desiredkey > currentNode→key):
# Visit right child, repeat
BST Search Runtime
Searching a BST in the worst case requires H + 1 comparisons, meaning O(H) comparisons, where H is the tree height.
Ex) A tree with a root node and one child node has height 1; the worst case visits the root and the child: 1 + 1 = 2
A major BST benefit is that an N-node binary tree's height may be as small as O(logN), uielding fast searches.
Ex) A 10,000 node list may requrie 10,000 comparisons at worst, but a 10,000 node BST may require only 14 comparisons.
A binary tree's height can be minimized by keeping all levels full, except possibly the last level.
Such an "all-but-last-level-full" binary tree's height is H = [log2(N)] where N = # of nodes.
In summary,
For a perfect BST, the worst case number of comparisons is [log2(n)] + 1, and have O(log2(N)) runtime complexity.
For a non-perfect BST, the worst case number of comparisons is H + 1, and have O(H) runtime complexity.
Successors and Predecessors
A BST defines an ordering among nodes, from smallest to largest.
A BST node's successor is the node that comes after in the BST ordering, so in A B C, A's successor is B, and B's successor is C.
A BST node's predecessor is the node that comes before in the BST ordering.

If a node has a right subtree, the node's successor is that right subtree's leftmost child: Starting from the right subtree's root, follow left children until reaching a node with no left child (may be that subtree's root itself). If a node doesn't have a right subtree, the node's successor is the first ancestor having this node in a left subtree. Another section provides an algorithm for printing a BST's nodes in order.