| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Object Oriented Programming
- 알고리즘
- assignment operator
- 함수
- 오블완
- const
- predictive analysis
- Pre-processing
- 포인터
- 백준
- OOP
- vscode
- 문자열
- baekjoon
- C++
- pointer
- 파이썬
- array
- Data Science
- Class
- raw data
- pass by reference
- Python
- function
- 배열
- Deep Learning
- 티스토리챌린지
- programming
- 반복문
- string
- Today
- Total
Channi Studies
Euler's Method | 오일러 방법 본문
Euler's Method, 오일러 방법은 미분방정식의 해를 근사치로 구하는 recursive numerical analysis method 입니다.
프로그래밍에 익숙한 학생들은 recursive function을 생각하면 정확히 같습니다.
Given dy/dx = f(x, y) 에서, f(x, y) 는 dy/dx 이기 때문에 그 자체로 방정식의 해 y = f(x) 의 기울기 (slope)를 나타냅니다.
그리고 주어진 initial value가 y(x₀) = y₀ 이라고 했을 때, 다음과 같은 관계가 성립합니다.
y_(n + 1) = y_n + h * f(x_n, y_n)
예를 들어 x₀ = 2, y₀ = 3 이 주어졌다면,
y₁ = y₀ + h * f(x₀, y₀) = 3 + h * f(2, 3) 이 되겠습니다.
위 recursive 공식에서 h 빼고 알겠는데, h는 무엇일까요?
h 는 increment of x 값 입니다.
x_(n+1) = x_n + h
의 관계가 이루어져 있고, 왜 이러한 식이 나왔는지는 다음 그림에서 볼 수 있습니다.
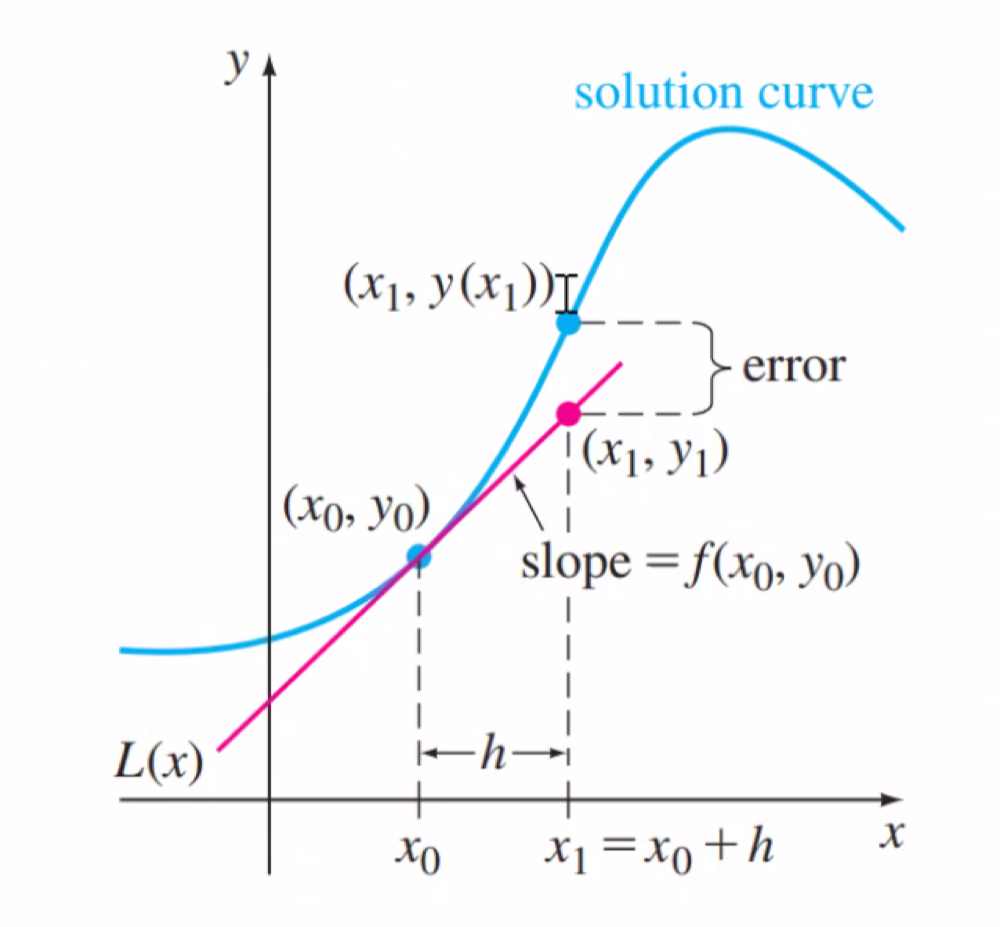
푸른색 Solution curve에 대해서 우리는 두개의 initial value x₀, y₀와 (x, y)에서의 solution's slope, f(x, y)도 알고 있습니다.
그렇다면, 현재 위치 (y_n) + 거리 (h) * 현재 기울기 (f(x_n, y_n)) 를 하면 대략적은 다음 점의 위치를 알 수 있지 않을까요?
해당 식의 도출 과정은 그리 이해하기 어렵지 않기 때문에 조금만 살펴보면 이해할 수 있습니다.
Excel Example
과연 그렇다면 Euler's Method가 얼마나 효과적인 approximation method인지 알아보도록 하겠습니다.
프로그램을 직접 작성해도 좋지만, 시각적으로 보기 쉽기 위해서 Google Sheet를 활용해보겠습니다.
우리가 살펴볼 문제는 다음과 같습니다.
dy/dx = 0.2xy, y(1) = 3
우리는 이 separable equation을 바로 풀 수 있겠죠?
풀이는 다음과 같습니다.
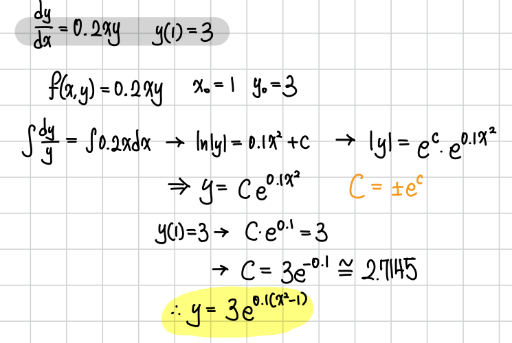
답은 y = 3e^(0.1(x^2-1)) 이라는 것을 구했습니다.
그렇다면 이제 google sheets에서 Euler's method를 적용하여 근사치를 구해보겠습니다.
여기서 h의 값을 아직 정하지 않았는데, 총 두가지 0.1 과 0.05 로 나누어서 두번의 시도를 해보겠습니다.
| Trial 1 (h = 0.1) | ||||||
| n | x_n | y_n (근사치) | y (실제 값) | abs. err. | rel. err. | h |
| 0 | 1.0 | 3.00000 | 3.00000 | 0.00000 | 0.000 | 0.1 |
| 1 | 1.1 | 3.06000 | 3.06367 | 0.00367 | 0.120 | |
| 2 | 1.2 | 3.12732 | 3.13495 | 0.00763 | 0.243 | |
| 3 | 1.3 | 3.20238 | 3.21431 | 0.01193 | 0.371 | |
| 4 | 1.4 | 3.28564 | 3.30228 | 0.01664 | 0.504 | |
| 5 | 1.5 | 3.37764 | 3.39945 | 0.02181 | 0.642 | |
첫번째 시도입니다.
h = 0.1 로 값을 잡고 시행을 했는데, 근사치가 실제 값과 상당히 유사하다는 것을 알 수 있죠?
0.5의 거리를 두고 h = 0.1 인 상태에서 해당 함수의 오차를 확인해보니, 절대오차 0.02, 상대오차 0.64%가 발생했네요.
두번째 시도입니다.
절반의 값 h = 0.05 로 시행한 결과, 근사치가 이번에는 기존보다 2배가량 더 유사하게 나온 것 같습니다.
0.5의 거리를 두고 h = 0.05 로 오일러 방법을 시행하자, 해당 함수에서는 상대 오차가 0.3% 밖에 발생하지 않았습니다.
| Trial 2 (h = 0.01) | ||||||
| n | x_n | y_n | y | abs. err. | rel. err. | h |
| 0 | 1.00 | 3.00000 | 3.00000 | 0.00000 | 0.000 | 0.05 |
| 1 | 1.05 | 3.03000 | 3.03091 | 0.00091 | 0.030 | |
| 2 | 1.10 | 3.06182 | 3.06367 | 0.00185 | 0.060 | |
| 3 | 1.15 | 3.09549 | 3.09833 | 0.00283 | 0.091 | |
| 4 | 1.20 | 3.13109 | 3.13495 | 0.00385 | 0.123 | |
| 5 | 1.25 | 3.16867 | 3.17359 | 0.00492 | 0.155 | |
| 6 | 1.30 | 3.20827 | 3.21431 | 0.00603 | 0.188 | |
| 7 | 1.35 | 3.24998 | 3.25718 | 0.00720 | 0.221 | |
| 8 | 1.40 | 3.29386 | 3.30228 | 0.00842 | 0.255 | |
| 9 | 1.45 | 3.33997 | 3.34967 | 0.00970 | 0.290 | |
| 10 | 1.50 | 3.38840 | 3.39945 | 0.01104 | 0.325 | |
이렇듯 오일러 방법은 매우 직관적이면서 실용적으로 활용될 수 있는 간단한 미분 방정식 해의 근사치를 구하는 방법입니다.
오일러 방법보다 여러가지 더욱 실제 해와 매우 근사하게 구할 수 있는 수학적 방법들이 많이 있지만, 여전히 꽤나 훌륭한 근사를 보여줍니다.
'기타 공부' 카테고리의 다른 글
| [PHYS II] Magnetic force per length example problem (0) | 2025.05.22 |
|---|

