| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- pass by reference
- programming
- 파이썬
- 오블완
- Pre-processing
- vscode
- array
- 티스토리챌린지
- 문자열
- Python
- pointer
- 반복문
- 백준
- const
- baekjoon
- 함수
- predictive analysis
- 배열
- OOP
- raw data
- Object Oriented Programming
- function
- Deep Learning
- Class
- 포인터
- Data Science
- assignment operator
- 알고리즘
- string
- C++
- Today
- Total
Channi Studies
[Data Structure] Treaps | 트립 본문
Treap Basics
A BST built from inserts of N nodes having random-ordered keys stays well-balanced and thus has near-minimum height, meaning searches, inserts, and deletes are O(logN).
Because insertion order may not be controllable, a data structure that somehow randomizes BST insertions is desirable.
A treap uses a main key that maintains a binary search tree oderering property, and a secondary key generated randomly (often called "priority") during insertions that maintains a heap property. The combination usually keeps the tree balanced. The word "treap" is a mix of tree and heap.
Algorithms for basic treap operation include:
- A treap search is the same as BST search using the main key, since the treap is a BST.
- A treap insert initially inserts a node as in a BST using the main key, then assigns a random priority to the node, and percolates the node up until the heap property is not violated. In a heap, a node is moved up via a wap with the node's parent. In a treap, a node is moved up via a rotation at the parent. Unlike a swap, a rotation maintains the BST property.
- A treap delete can be done by setting the node's priority such that the node should be a leaf (-∞ to max-heap), percolating the node down using rotations untiul the node is a leaf, and then removing the node.

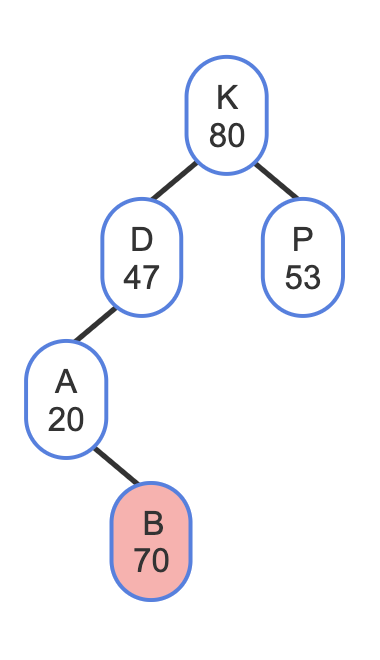

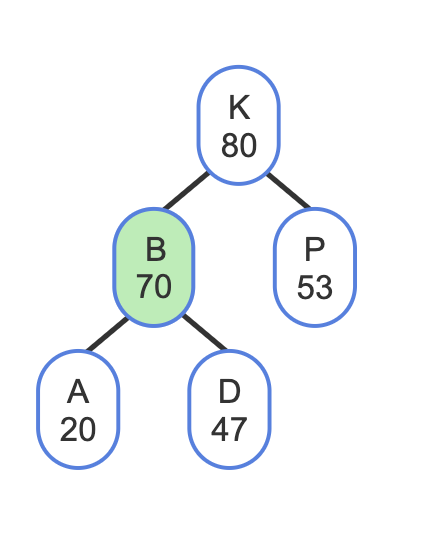
Treap Delete
A treap delete could be done by first doing a BST delete (copying the successor to the node-to-delete, then deleting the original successor), followed by percolating the node down until the heap property is not violated. However, a simpler approach just sets the node-to-delete's priority to -∞ (for a max-heap), percolates the node down until a leaf, and removes the node. Percolating the node down uses rotations, not swaps, to maintain the BST property. Also, the node is rotated in the direction of the lower-priority child, so that the node rotated up has a higher priority than that child, to keep the heap property.
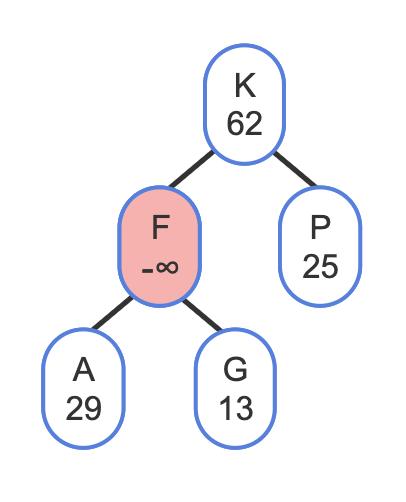


Q: Suppose a treap is built by inserting nodes with main keys in this order: A, B, C, D, E, F, G. The treap will have 7 levels, with each level having one node with a right child. (True/False)
A: A BST would have such a structure, but it's treap. It assigns random priority for each node, so after insertion the nodes will be rearranged following to the heap property on the priority value.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [ADT] Set - 2 | Set Opeartions (0) | 2025.05.15 |
|---|---|
| [ADT] Set - 1 (0) | 2025.05.15 |
| [ADT] Priority Queue Abstract Data Type (0) | 2025.05.09 |
| Abstract Data Type (ADT) V.S. Data Structure | 추상 자료형 vs 자료 구조형 (0) | 2025.05.09 |
| [Data Structure] Heap Sort (0) | 2025.05.08 |




