| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Python
- 배열
- vscode
- string
- const
- Deep Learning
- programming
- 파이썬
- Data Science
- array
- OOP
- 오블완
- pass by reference
- 백준
- 문자열
- raw data
- 알고리즘
- Pre-processing
- Object Oriented Programming
- 반복문
- 함수
- 포인터
- C++
- Class
- 티스토리챌린지
- predictive analysis
- assignment operator
- baekjoon
- function
- pointer
- Today
- Total
Channi Studies
Linear Regression (선형 회귀) - 7 | Adjusted R-Squared (수정된 결정 계수) 본문
Linear Regression (선형 회귀) - 7 | Adjusted R-Squared (수정된 결정 계수)
Chan Lee 2024. 6. 12. 06:17지난 포스트에서는 R-squared, 결정 계수에 대해서 알아보았습니다.
이는 우리의 회귀 모델이 실제 데이터의 분산을 얼마나 잘 설명하는지를 나타낸 값으로, SST/SSR 이였습니다.
Linear Regression (선형 회귀) - 6 | R-Squared (결정 계수)
지난 포스트에서는 OLS, 최소 제곱법에 대해서 간단하게 알아보았습니다. Linear Regression (선형 회귀) - 5 | Ordinary Least Squares (최소제곱법)저번 포스트에서는 SST, SSR, SSE의 관계에 대해서 알아보았습
code-studies.tistory.com
이번 포스트에서는 수정된 결정계수, Adjusted R Squared에 대해서 알아보겠습니다.

우리가 자주 보던 이 Regerssion summary table에는, 저번에 확인한 R-squared 값이 나타나 있습니다.
그 바로 밑에는 Adj. R-squared, 즉 수정된 결정 계수 값이 있습니다.
이 수정된 결정 계수는 도대체 뭘까요?
이를 알기 위해서는, 우선 R-squared의 한계를 먼저 이해해야 합니다.
[아직 SST, SSR, SSE에 대해서 모르신다면 다음 포스트를 먼저 보고 와주세요]
Linear Regression (선형 회귀) - 4 | SST = SSR + SSE
저번 포스트에서는 선형 회귀 모델을 디자인 하는 과정에서 StatsModels 라이브러리를 활용하여 얻을 수 있는 Coefficient Table에 대해서 알아보았습니다. Linear Regression (선형 회귀) -3 | Coefficients Table
code-studies.tistory.com
R-Squared, 결정 계수의 식은 SSR/SST 이였고, SST는 (실제 y값 - 평균 y값)^2 의 총 합이였습니다.
여기서 독립 변수인 x가 아무리 늘어나도, 실제 y값과 평균 y값에는 당연히 아무 영향이 없겠죠?
즉, R- squared의 분모 부분은 변수를 아무리 늘려도 동일합니다.
반면, SSR는 설명된 분산으로, 변수가 늘면 늘수록 회귀 모델은 설명을 더 잘하면 잘했지 못하진 않겠죠?
실제로 변수가 늘어나면, SSR는 무조건 증가하거나 유지됩니다.
감소할수가 없어요.
이는 분수에서 분자의 증가나 유지, 그리고 분모의 무조건적인 유지를 의미하므로,
변수가 증가하면 결정계수는 무조건 증가하거나 유지됩니다.
그렇다면 만약 아무런 의미가 없고, 결과 예측에 도움이 되지가 않는 변수들만 잔뜩 추가하면 어떻게 될까요?
이 상황을 우리는 과적합 (Overfitting) 이라고 하며, 과적합된 모델은 학습된 데이터에서만 뛰어난 예측 성능을 발휘하고, 새로운 데이터에는 학습 성능이 지나치게 낮은 결과가 발생합니다.
자, 여기까지 R-squared의 한 가지 한계를 말씀드렸습니다.
그렇다면, Adjusted R-Squared는 당연히 이 문제를 해결하는 방법으로 디자인 되었겠죠?
물론입니다.
수정된 결정 계수는 무의미한 변수의 추가를 penalize하게끔 디자인 되어 있습니다.
즉, 무의미한 변수가 많을수록 adjusted r-squared는 감소합니다.
이러한 이유로 adjusted r-squared는 거의 무조건 r-squared보다 작습니다.
다시 처음의 표로 돌아가겠습니다.

이제 우리는 왜 adjusted r-squared가 더 작은지, 그리고 이것이 무엇을 의미하는지를 배웠습니다.
그렇다면, 어떤 변수가 무의미한지를 직감 말고 데이터로 확실하게 확인할 방법은 없을까요?
표의 아래 부분을 살펴보겠습니다.
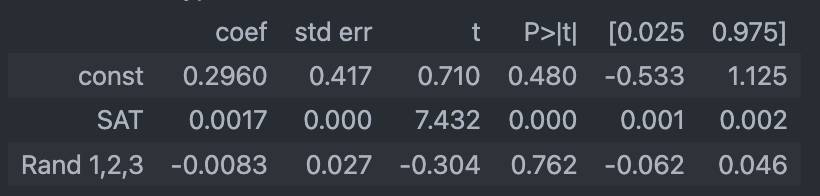
위 값은 수능 성적으로 대학 학점을 예측하는 단순 선형회귀 모델에서, 무의미한 랜덤 정수 1, 2, 3을 표현하는 변수 하나를 추가한 모델입니다.
여기서 우리가 볼 것은 p-value를 나타내는 P>|t| 의 값입니다.
가설 검정 할 때, p-value가 5%, 0.05보다 작으면 통계적으로 유의미한 데이터라고 간주했던거, 기억 나시나요?
SAT의 경우에는 0.000으로 매우 유의미하게 대학 성적을 예측한다고 이해할 수 있습니다.
반면 Rand 1,2,3으로 이름 붙여진 랜덤 정수값들의 경우에는 무려 0.762로, 매우 무의미한 값임을 나타내고 있습니다.
즉, 이로써 우리는 여러가지 변수가 주어졌을 때, 회귀 모델에서의 p-value를 기반으로 어떠한 값이 잘 데이터를 설명하고 예측하는지에 대해서 알 수 있겠습니다.
마지막으로 간단하게, F-Statistic에 대해서도 알아보겠습니다.
이름에서 유추하듯 T-Statistic, Z-Statistic 처럼 확률 분포에서 가설 검정할 때 사용합니다.

F-Statistic의 Null hypothesis는 다음과 같습니다.
H0: B1 = B2 = B3 = ... = Bk = 0
H1: At least one is different
즉, 우리의 '모든 독립 변수들이 무의미하다' 가 Null hypothesis가 되겠구요,
단 하나라도 유의미하다는게 Alternative Hypothesis가 되겠습니다.
F-Statistic 값이 0에 가까울 수록 Null을 부정하지 못할 확률이 늘어납니다.
해석을 편하게 하기 위해서, F-Statistic 밑에 이를 P-value로 변환한 값을 보는 것이 편합니다.
역시 0.05를 significance level로 하고, 0.05보다 작으면 최소 1개 이상이 유의미하다고 해석할 수 있겠네요.
'Data Science > 개념과 용어' 카테고리의 다른 글
| What is Data Science? (1) | 2024.09.09 |
|---|---|
| Linear Regression (선형 회귀) - 8 | Assumptions (선형 회귀 가정) (1) | 2024.06.12 |
| Linear Regression (선형 회귀) - 6 | R-Squared (결정 계수) (1) | 2024.06.03 |
| Linear Regression (선형 회귀) - 5 | Ordinary Least Squares (최소제곱법) (1) | 2024.06.03 |
| Linear Regression (선형 회귀) - 4 | SST = SSR + SSE (1) | 2024.06.03 |



