| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- assignment operator
- 알고리즘
- 오블완
- const
- pass by reference
- 백준
- function
- vscode
- array
- predictive analysis
- Python
- string
- OOP
- C++
- raw data
- 파이썬
- 문자열
- 배열
- Deep Learning
- Pre-processing
- Data Science
- programming
- 함수
- 반복문
- Class
- 포인터
- baekjoon
- pointer
- 티스토리챌린지
- Object Oriented Programming
- Today
- Total
Channi Studies
[Sorting] Radix Sort 본문
Radix Sort
Radix sort is a sorting algorithm designed specifically for integers.
Buckets
Radix sort algorithm makes use of a concept called buckets and is a type of bucket sort.
Any array of integer values can be subdivided into buckets by using the integer values' digits.
A bucket is a collection of integer values that all share a particular digit value.
Ex: Values 57, 97, 77, and 17 all have a 7 as the 1's digit, and would all be placed into bucket 7 when subdividing by the 1's digit.
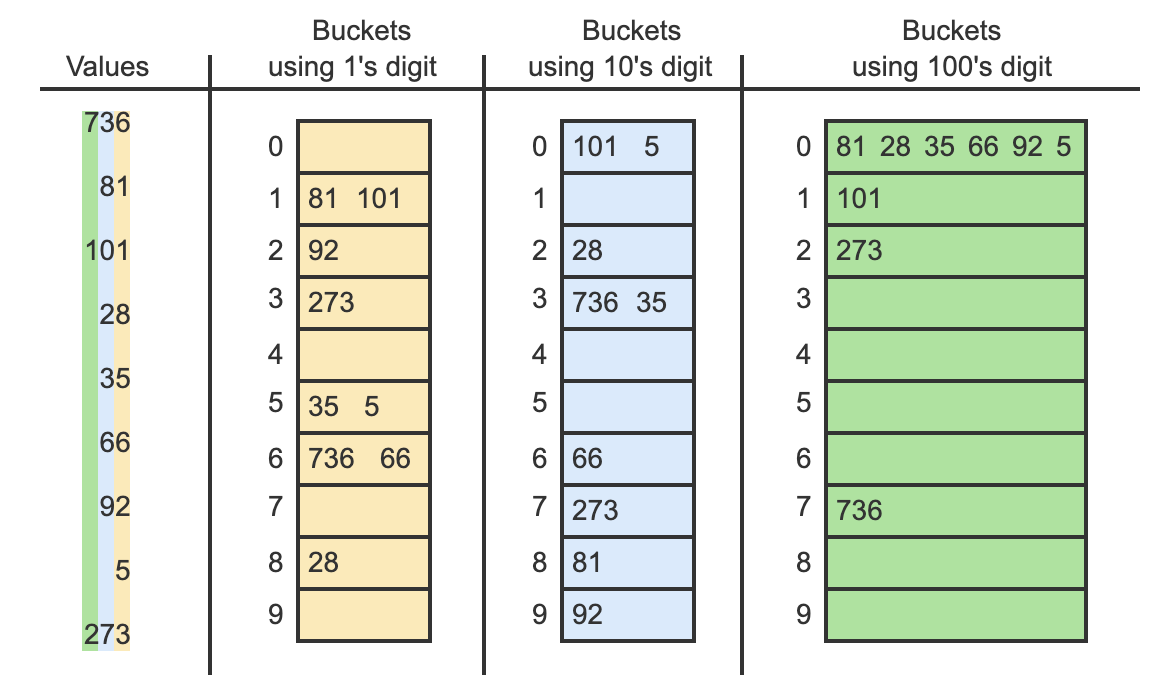
So, even if a value is in a lower bucket, it does not always mean that the actual data is lower than the other. (ex. 736 in bucket 6, but 5 in bucket 5 for the buckets using 1's digit)
Now since we've understood the notion of bucket, let's look into the actual algorithm with Python code.
Radix Sort Algorithm & Python Implementation
Radix sort is a sorting algorithm specifically for an array of integers: The algorithm processes one digit at a time starting with the least significant digit and ending with the most significant.
Two steps are needed for each digit.
First, all array elements are placed into buckets based on the current digit's value.
Then, the array is rebuilt by removing all elements from buckets, in order from lowest bucket to highest.
The radix_sort() function below has one parameter, numbers, which is an unsorted list of integers.
A list is a mutable object, so changes to numbers inside the function will all affect any variable that references that list.
A list of 10 lists is used for the buckets. The radix_get_max_length() function determines the number of relevant powers of 10. The digit-index loop then iterates through those powers of 10. The first inner loop places the elements into buckets based on the current power of 10. The second inner loop moves elements out of buckets and back into the numbers list, in order from lowest bucket index to highest. After the digit-index loop, two new lists are built, one containing all negative elements from the numbers list and the other containing all non-negative elements. Then, the reversed negative list is concatenated with the non-negative list into the numbers list to produce the sorted result.
## Radix Sort
def radix_get_max_length(numbers: list[int]) -> int:
# Returns the maximum length, in number of digits, out of all list elements
max_digits = 0
for num in numbers:
digit_count = radix_get_length(num)
if digit_count > max_digits:
max_digits = digit_count
return max_digits
def radix_get_length(value: int) -> int:
# Returns the length, in number of digits, of value
if value == 0:
return 1
digits = 0
while value != 0:
digits += 1
value = value // 10
return digits
def radix_sort(numbers: list[int]) -> None:
buckets = []
for i in range(10):
buckets.append([])
# Find the max length, in number of digits
max_digits = radix_get_max_length(numbers)
pow_10 = 1
for digit_index in range(max_digits):
for num in numbers:
bucket_index = (abs(num) // pow_10) % 10
buckets[bucket_index].append(num)
numbers.clear()
for bucket in buckets:
numbers.extend(bucket)
bucket.clear()
pow_10 *= 10
negatives = []
non_negatives = []
for num in numbers:
negatives.append(num) if num < 10 else non_negatives.append(num)
negatives.reverse()
numbers.clear()
numbers.extend(negatives + non_negatives)
In this code, we included an algorithm to handle negative values at the final part.
Negative values will be erroneously sorted into based on its absolute values.
So we partition them again based on their signs, reverse the negative partition, and re-merge it together.
Radix Sort Runtime Complexity
Radix sort's worst runtime complexity is O(n), which is very efficient.
Also, radix sort has a space complexity of O(n) since we need to create the bucket array, proportionally larger to the original array.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] List Abstract Data Type (ADT) (0) | 2025.03.27 |
|---|---|
| [Sorting] Fast Sorting Algorithms & Sorting in Python (0) | 2025.03.19 |
| [Sorting] Merge Sort (0) | 2025.03.18 |
| [Sorting] Quick Sort (0) | 2025.03.17 |
| [Sorting] Shell Sort (0) | 2025.03.17 |




