| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- raw data
- pass by reference
- vscode
- 파이썬
- 배열
- Data Science
- predictive analysis
- array
- Deep Learning
- string
- Python
- 함수
- programming
- OOP
- 오블완
- Object Oriented Programming
- pointer
- 알고리즘
- 포인터
- C++
- assignment operator
- 백준
- function
- const
- 티스토리챌린지
- baekjoon
- Class
- Pre-processing
- 문자열
- 반복문
- Today
- Total
Channi Studies
[Sorting] Quick Sort 본문
Quick Sort
Quick sort is a sorting algorithm that repeatedly partitions the input into low and high parts (each part unsorted), and then recursively sorts each of those parts.
To partition the input, quicksort chooses a pivot to divide the data into low and high parts.
The pivot can be any value within the array being sorted, commonly the value of the middle array element.
Ex: For the list (4, 34, 10, 25, 1), the middle element is located at index 2 (the middle of indices [0, 4]) and has a value of 10.
Once the pivot is chosen, the quicksort algorithm divides the array into two parts, referred to as the low partition and the high partition.
All values in the low partition are less than or equal to the pivot value.
All values in the high partition are greater than or equal to the pivot value.
The values in each partition are not necessarily sorted.
Ex: Partitioning (4, 34, 10, 25, 1) with a pivot value of 10 results in a low partition of (4, 1, 10) and a high partition of (25, 34). Values equal to the pivot may appear in either or both of the partitions.
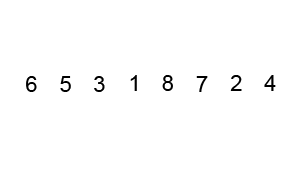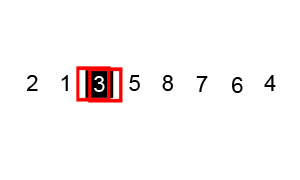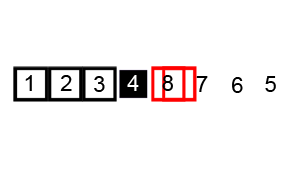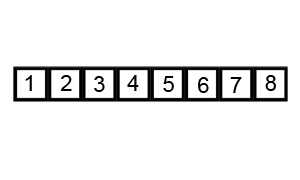
This could be a confusing algorithm.
Let's look into Python code to get a better understanding.
Python Implementation
We will be using two separate functions each for partitioning and quick sorting.
# Quick Sort
def partition(numbers: list[int], start_index: int, end_index: int) -> int:
# Select the middle value as the pivot.
midpoint = (start_index + end_index) // 2
pivot = numbers[midpoint]
# low and high starts at each end of the list segment, moving towards each other
low_index, high_index = start_index, end_index
done = False
while not done:
while (pivot > numbers[low_index]): low_index += 1
while (pivot < numbers[high_index]): high_index -= 1
# If low and high crossed each other, the loop is done.
# If not, the element is swapped, low_index is incremented, and high_index is decremented.
if low_index >= high_index:
done = True
else:
numbers[low_index], numbers[high_index] = numbers[high_index], numbers[low_index]
low_index += 1
high_index -= 1
return high_index
def quicksort(numbers: list[int], start_index: int, end_index: int) -> None:
# Only attemp to sort the list if there are at least 2 elements
if end_index <= start_index: return
# Partition the list segment
high = partition(numbers, start_index, end_index)
# Recursively sort the left segment
quicksort(numbers, start_index, high)
# Recursively sort the right segment
quicksort(numbers, high + 1, end_index)
Runtime Complexity
The runtime complexity for quick sort is typically O(N log N).
There will be total log2(N) partitioning levels and at most N comparisons at each level.
However, for the worst case where the pivot selected for partitioning is always the smallest or largest element, one partition will have only one element (itself), and the other partition will have all remaining elements.
In that worst case, there will be N - 1 partitioning levels, yielding O(N) = O(N(N+1)/2) = O(N²).
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Sorting] Radix Sort (0) | 2025.03.18 |
|---|---|
| [Sorting] Merge Sort (0) | 2025.03.18 |
| [Sorting] Shell Sort (0) | 2025.03.17 |
| [Sorting] Insertion Sort (0) | 2025.03.17 |
| [Sorting] Introduction & Selection Sort (0) | 2025.03.16 |



