| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- predictive analysis
- function
- Data Science
- 티스토리챌린지
- 배열
- Deep Learning
- 포인터
- pointer
- C++
- const
- Python
- 오블완
- array
- 반복문
- programming
- Pre-processing
- OOP
- baekjoon
- 백준
- 함수
- string
- assignment operator
- 파이썬
- pass by reference
- vscode
- Class
- 알고리즘
- raw data
- 문자열
- Object Oriented Programming
- Today
- Total
Channi Studies
[Sorting] Merge Sort 본문
In the previous post, we have looked into quick sort and shell sort.
[Sorting] Shell Sort
In the final post, we looked into the selection sorting algorithm.https://code-studies.tistory.com/124 [Sorting] Insertion SortIn the final post, we have studied about the selection sort and its implementation in Python. https://code-studies.tistory.co
code-studies.tistory.com
[Sorting] Quick Sort
Quick Sort Quick sort is a sorting algorithm that repeatedly partitions the input into low and high parts (each part unsorted), and then recursively sorts each of those parts. To partition the input, quicksort chooses a pivot to divide the data into low
code-studies.tistory.com
In this post, we are going to learn about new type of sorting algorithm, called merge sort!
Merge Sort
Merge sort is a sorting algorithm that divides a list into two halves, recursively sorts each half, and then merges the sorted halves to produce a sorted list.
The recursive partitioning continues until a list of 1 element is reached, as a list of 1 element is already sorted.
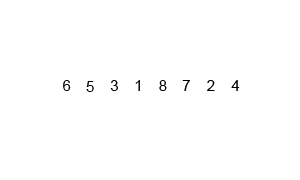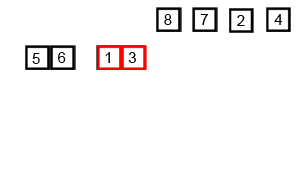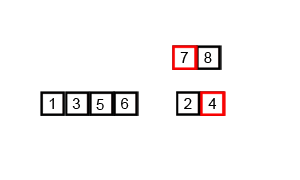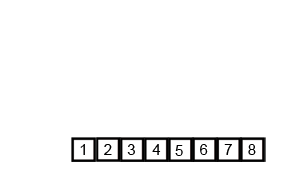
Since we need partitioning algorithm as we did in the quick sort to perform a merge sort, we will first look at the partitioning algorithm.
Partitioning Algorithm
The merge sort algorithm uses three index variables to keep track of the elements to sort for each recursive function call.
The index variable i is the index of first element in the list, and the index variable k is the index of the last element.
The index variable j is used to divide the list into two halves.
Elements from i to j are in the left half, and elements from j + 1 to k are in the right half.
So for example, if we have numbers = [1, 2, 3, 4, 5], i=0, k=4,
j = (i + k) // 2 = (0 + 4) // 2 = 2
Left Partition = numbers[i : j+1] = [1, 2, 3]
Right Partition = numbers[j+1 : k] = [4, 5]
Another example with numbers = [34, 78, 14, 23, 8, 35], i = 3, k = 5,
j = (3 + 5) // 2 = 4
Left partition = [23, 8]
Right partition = [35]
Now, since the array is partitioned, now we have to merge it back while sorting it!
Let's check how we can do it.
Merge Sort Algorithm
The merging + sorting algorithm, merge sort algorithm, merges the two sorted partitions into a single list by repeatedly selecting the smallest element from either the left or right partition and adding that element to a temporary merged list.
Once fully merged, the elements in the temporary merged list are copied back to the original list.
This website provides a step by step merge sort algorithm visualization.
Merge Sort visualize | Sorting | Algorithms | HackerEarth
Visualize your learning on Merge Sort to improve your understanding of Algorithms.
www.hackerearth.com
Let's check out Python code.
Python Implementation
Merge sort is a sorting algorithm that divides a list into two halves, recursively sorts each half, and then merges the sorted halves to produce a sorted list.
Merge sort uses 2 functions: merge() and merge_sort().
The merge() function merges 2 sequential, sorted partitions within a list and has 4 parameters:
- The list of numbers containing the 2 sorted partitions to merge
- The start index of the first sorted partition
- The end index of the first sorted partition
- The end index of the second sorted partition
The merge_sort() function sorts a partition in a list and has 3 parameters:
- The list containing the partition to sort
- The start index of the partition to sort
- The end index of the partition to sort
If the partition size is greater than 1, the merge_sort() function recursively sorts the left and right halves of the partition, then merges the sorted halves together.
When the start index is 0 and the end index is the list length minus 1, merge_sort() sorts the entire list.
# Merge Sort
def merge(numbers: list[int], i: int, j: int, k: int):
"""merge left and right partitions
@param i: first index of the left partition
@param j: last index of the left partition
@param k: last index of the right partition"""
merged_size = k - i + 1 # Size of the merged partition
merged_numbers = [0] * merged_size # Dynamically allocates temporary array (list)
merge_pos = 0 # Position to insert merged number
left_pos = i # Initialize left partition position
right_pos = j + 1 # Initialize right partition position
# Add smallest element from left or right partition to merged numbers
while left_pos <= j and right_pos <= k:
if numbers[left_pos] <= numbers[right_pos]:
merged_numbers[merge_pos] = numbers[left_pos]
left_pos += 1
else:
merged_numbers[merge_pos] = numbers[right_pos]
right_pos += 1
merge_pos += 1
# If left partition is not empty, add remaining elements to merged numbers
while left_pos <= j:
merged_numbers[merge_pos] = numbers[left_pos]
left_pos += 1
# If right partition is not empty, add remaining elements to merged numbers
while right_pos <= j:
merged_numbers[merge_pos] = numbers[right_pos]
right_pos += 1
# Copy number back to numbers
for merge_pos in range(merged_size):
numbers[merge_pos] = merged_numbers[merge_pos]
def merge_sort(numbers, i, k):
j = 0
if i < k:
# Find the midpoint in the partition (largest index of the left partition)
j = (i + k) // 2
# Recursively sort left and right partitions
merge_sort(numbers, i, j)
merge_sort(numbers, j+1, k)
# Merge left and right partitions in sorted order
merge(numbers, i, j, k)
Runtime Complexity
The runtime complexity of merge sort is O(n log n).
Merge sort divides the input in half until a list of 1 element is reached, which requires log N partitioning levels.
At each level, the algorithm does about N comparisons selecting and copying elements from the left and right partitions, yielding N * log N comparisons.
Merge sort requires O(N) additional memory elements for the temporary array of merged elements.
For the final merge operation, the temporary list has the same number of elements as the input.
Some sorting algorithms sort the list elements in place and require no additional memory, but are more complex to write and understand.
At this point in my opinion, it is rather important to understand and memorize the concept of the sorting algorithm, rather than the direct implementation of the code.
In the next post, we will look into the final sorting algorithm, Radix Sort.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Sorting] Fast Sorting Algorithms & Sorting in Python (0) | 2025.03.19 |
|---|---|
| [Sorting] Radix Sort (0) | 2025.03.18 |
| [Sorting] Quick Sort (0) | 2025.03.17 |
| [Sorting] Shell Sort (0) | 2025.03.17 |
| [Sorting] Insertion Sort (0) | 2025.03.17 |



