| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- const
- Data Science
- assignment operator
- predictive analysis
- Deep Learning
- string
- 함수
- 티스토리챌린지
- baekjoon
- raw data
- programming
- 포인터
- function
- 오블완
- 파이썬
- 백준
- 문자열
- Class
- array
- Python
- Object Oriented Programming
- 알고리즘
- vscode
- 배열
- OOP
- pointer
- C++
- pass by reference
- Pre-processing
- 반복문
- Today
- Total
Channi Studies
[Data Structure] Binary Search Trees 본문
[Data Structure] Binary Search Trees
Chan Lee 2025. 4. 22. 02:44Binary Search Trees
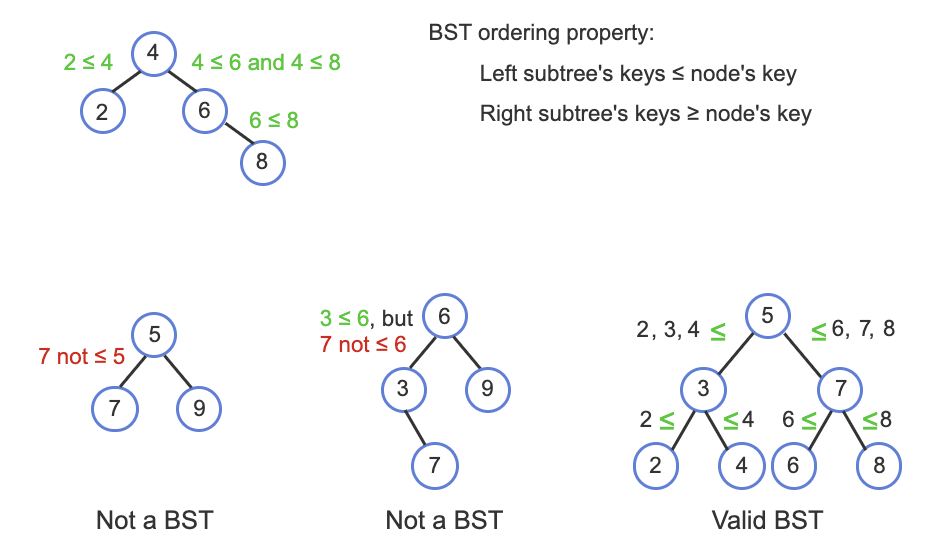
An especially useful form of binary tree is a binary serach tree (BST).
BST has an ordering property that any node's left subtree keys ≤ the node's key and the right subtree's keys ≥ the node's key.
This property enables fast searching for an item.
Searching
To search nodes means to find a node with a desired key, if such a node exists.
A BST may yield faster searches than a list.
Searching a BST starts by visiting the root node.
# Pseudocode for Search
if (currentNode→key == desiredkey):
return currentNode
else if (desiredkey < currentNode→key):
# Visit left child, repeat
else if (desiredkey > currentNode→key):
# Visit right child, repeat
BST Search Runtime
Searching a BST in the worst case requires H + 1 comparisons, meaning O(H) comparisons, where H is the tree height.
Ex) A tree with a root node and one child node has height 1; the worst case visits the root and the child: 1 + 1 = 2
A major BST benefit is that an N-node binary tree's height may be as small as O(logN), uielding fast searches.
Ex) A 10,000 node list may requrie 10,000 comparisons at worst, but a 10,000 node BST may require only 14 comparisons.
A binary tree's height can be minimized by keeping all levels full, except possibly the last level.
Such an "all-but-last-level-full" binary tree's height is H = [log2(N)] where N = # of nodes.
In summary,
For a perfect BST, the worst case number of comparisons is [log2(n)] + 1, and have O(log2(N)) runtime complexity.
For a non-perfect BST, the worst case number of comparisons is H + 1, and have O(H) runtime complexity.
Successors and Predecessors
A BST defines an ordering among nodes, from smallest to largest.
A BST node's successor is the node that comes after in the BST ordering, so in A B C, A's successor is B, and B's successor is C.
A BST node's predecessor is the node that comes before in the BST ordering.

If a node has a right subtree, the node's successor is that right subtree's leftmost child: Starting from the right subtree's root, follow left children until reaching a node with no left child (may be that subtree's root itself). If a node doesn't have a right subtree, the node's successor is the first ancestor having this node in a left subtree. Another section provides an algorithm for printing a BST's nodes in order.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] BST Inorder Traversal, Height, and Insertion Order (0) | 2025.04.22 |
|---|---|
| [Data Structure] BST Operations - Search, Insert, and Remove (0) | 2025.04.22 |
| [Data Structures] Binary Tree - 2 | Application of Trees (File Systems, BSP) (0) | 2025.04.22 |
| [Data Structures] Binary Trees - 1 (0) | 2025.04.22 |
| [Data Structure] Hash Table - 6 | Python Implementation (0) | 2025.04.10 |




