| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 알고리즘
- 배열
- pass by reference
- const
- Deep Learning
- Python
- vscode
- Data Science
- programming
- 함수
- C++
- OOP
- array
- Pre-processing
- predictive analysis
- 파이썬
- 티스토리챌린지
- Class
- 오블완
- function
- 포인터
- string
- 백준
- raw data
- assignment operator
- 반복문
- 문자열
- pointer
- baekjoon
- Object Oriented Programming
- Today
- Total
Channi Studies
[Data Structure] BST Operations - Search, Insert, and Remove 본문
[Data Structure] BST Operations - Search, Insert, and Remove
Chan Lee 2025. 4. 22. 04:33Search
Given a key, a search algorithm returns the first node found matching that key, or returns null if a matching node is not found.
A simple BST search algorithm checks the current node (initially the tree's root node), returning that node as a match, else assigning the current node with the left (if key is less) or right (if key is greater) child and repeating.
If such a child is null, the algorithm returns null (matching node not found).
// BST Search pseudocode
BSTSearch(tree, key) {
cur = tree⇢root
while (cur is not null) {
if (key == cur⇢key) {
return cur // Found
}
else if (key < cur⇢key) {
cur = cur⇢left
}
else {
cur = cur⇢right
}
}
return null // Not found
}
Insert
Given a new node, a BST insert operation inserts the new node in a proper location obeying the BST ordering property.
A simple BST insert algorithm compares the new node with the current node (initially the root).
- Insert as left child: If the new node's key is less than the current node, and the current node's left child is null, the algorithm assigns that node's left child with the new node.
- Insert as right child: If the new node's key is greater than or equal to the current node, and the current node's right child is null, the algorithm assigns the node's right child with the new node.
- Search for insert location: If the left (or right) child is not null, the algorithm assigns the current node with that child and continues searching for a proper insert location.
// Pseudocode for Insert
BSTInsert(tree, node) {
if (tree⇢root is null) {
tree⇢root = node
}
else {
currentNode = tree⇢root
while (currentNode is not null) {
if (node⇢key < currentNode⇢key) {
if (currentNode⇢left is null) {
currentNode⇢left = node
currentNode = null
}
else {
currentNode = currentNode⇢left
}
}
else {
if (currentNode⇢right is null) {
currentNode⇢right = node
currentNode = null
}
else {
currentNode = currentNode⇢right
}
}
}
}
}
BST insertion has best case runtime complexity of O(log N) and worst case O(N).
Remove
Given a key, a BST remove operation removes the first-found matching node, restructuring the tree to preserve the BST ordering property. The algorithm first searches for a matching node just like the search algorithm. If found (call this node X), the algorithm performs one of the following sub-algorithms:
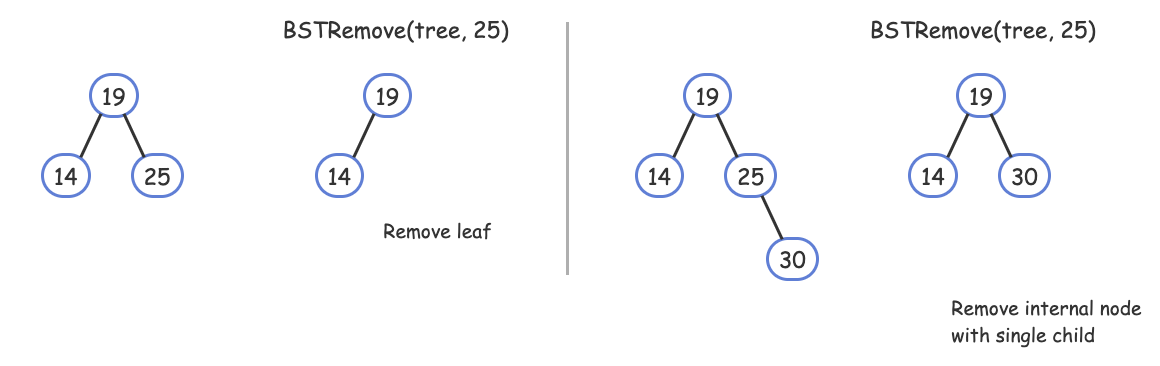
- Remove a leaf node: If X has a parent (so X is not the root), the parent's left or right child (whichever points to X) is assigned with null. Else, if X was the root, the root pointer is assigned with null, and the BST is now empty.
- Remove an internal node with single child: If X has a parent (so X is not the root), the parent's left or right child (whichever points to X) is assigned with X's single child. Else, if X was the root, the root pointer is assigned with X's single child.
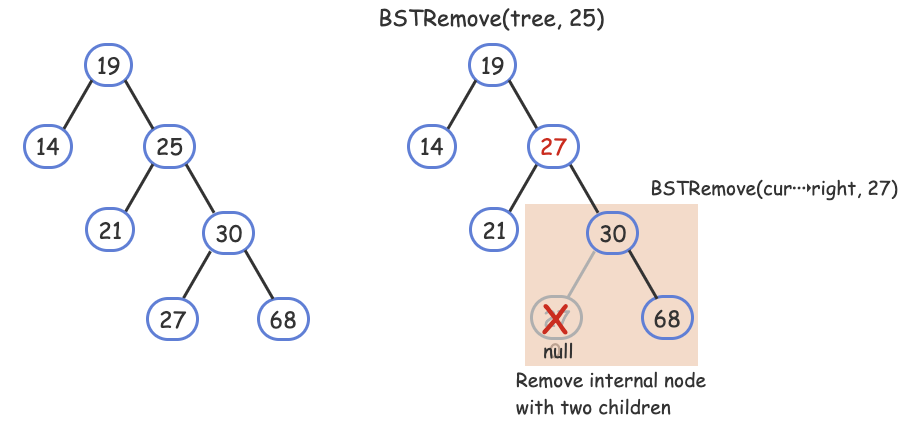
- Remove an internal node with two children: This case is the hardest. First, the algorithm locates X's successor (the leftmost child of X's right subtree), and copies the successor to X. Then, the algorithm recursively removes the successor from the right subtree.
// Pseudocode for Remove
BSTRemove(tree, key) {
parent = null
currentNode = tree⇢root
while (currentNode != null) {
// Check if currentNode has an equal key
if (currentNode⇢key == key) {
if (currentNode⇢left is null && currentNode⇢right is null) {
// Remove leaf
if (parent is null) { // Node is root
tree⇢root = null
}
else if (parent⇢left == currentNode) {
parent⇢left = null
}
else {
parent⇢right = null
}
return true // Node found and removed
}
else if (currentNode⇢right is null) {
// Remove node with only left child
if (parent is null) { // Node is root
tree⇢root = currentNode⇢left
}
else if (parent⇢left == currentNode) {
parent⇢left = currentNode⇢left
}
else {
parent⇢right = currentNode⇢left
}
return true // Node found and removed
}
else if (currentNode⇢left is null) {
// Remove node with only right child
if (parent is null) { // Node is root
tree⇢root = currentNode⇢right
}
else if (parent⇢left == currentNode) {
parent⇢left = currentNode⇢right
}
else {
parent⇢right = currentNode⇢right
}
return true // Node found and removed
}
else {
// Remove node with two children
// Find successor (leftmost child of right subtree)
successor = currentNode⇢right
while (successor⇢left is not null) {
successor = successor⇢left
}
// Copy successor's key to current node
currentNode⇢key = successor⇢key
Parent = currentNode
// Reassign currentNode and key so that loop continues with new key
currentNode = currentNode⇢right
key = successor⇢key
}
}
else if (currentNode⇢key < key) {
// Search right
parent = currentNode
currentNode = currentNode⇢right
}
else {
// Search left
parent = currentNode
currentNode = currentNode⇢left
}
}
return false // Node not found
}
A BST with N nodes has at least log₂N levels and at most N levels.
So removal's best case time complexity is O(logN) for a BST with log₂N levels and at most N levels, and worst case O(N) for a tree with N levels.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] BST Parent Node Pointers, and Recursion (0) | 2025.04.23 |
|---|---|
| [Data Structure] BST Inorder Traversal, Height, and Insertion Order (0) | 2025.04.22 |
| [Data Structure] Binary Search Trees (0) | 2025.04.22 |
| [Data Structures] Binary Tree - 2 | Application of Trees (File Systems, BSP) (0) | 2025.04.22 |
| [Data Structures] Binary Trees - 1 (0) | 2025.04.22 |



