Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 티스토리챌린지
- 배열
- Object Oriented Programming
- raw data
- 함수
- const
- 알고리즘
- Deep Learning
- Python
- 파이썬
- 백준
- Data Science
- string
- function
- pointer
- 반복문
- Class
- 포인터
- Pre-processing
- C++
- assignment operator
- programming
- vscode
- baekjoon
- predictive analysis
- 문자열
- 오블완
- array
- pass by reference
- OOP
Archives
- Today
- Total
Channi Studies
[Data Structure] Red-Black Tree - 1 본문
Data Science/Data Structure & Algorithm
[Data Structure] Red-Black Tree - 1
Chan Lee 2025. 5. 2. 11:14A red-black tree is a BST with two node types, namely red and black, and supporting operations that ensure the tree is balanced when a node is inserted or removed.
Rules:
- Every node is colored either red or black.
- The root node is black.
- A red node's children cannot be red.
- A null child is considered to be a black leaf node.
- All paths from a node to any null leaf descendant node must have the same number of black nodes.
These rules ensure that a tree with N nodes will have a height of O(log N).

After an insertion or removal of a node, the red-black tree can be unbalanced.
Same as AVL trees, red-black trees use rotations to rebalance the tree.
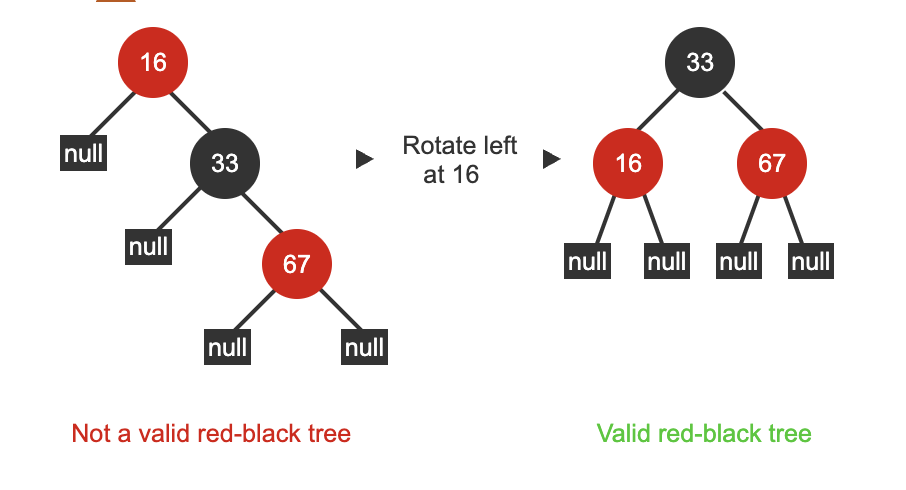
RBTreeRotateLeft(tree, node) {
rightLeftChild = node⇢right⇢left
if (node⇢parent != null)
RBTreeReplaceChild(node⇢parent, node, node⇢right)
else { // node is root
tree⇢root = node⇢right
tree⇢root⇢parent = null
}
RBTreeSetChild(node⇢right, "left", node)
RBTreeSetChild(node, "right", rightLeftChild)
}'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] Heaps - 1 | Max-heap (최대 힙) and Min-heap (최소 힙) (0) | 2025.05.08 |
|---|---|
| [Data Structure] Red-Black Tree - 2: Insertion & Balance (0) | 2025.05.02 |
| [Data Structure] AVL Tree - 3: AVL Insertions & Removals (0) | 2025.05.01 |
| [Data Structure] AVL Tree - 2: AVL Rotations (0) | 2025.05.01 |
| [Data Structure] AVL Tree - 1: Introduction (0) | 2025.05.01 |



