| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Object Oriented Programming
- Data Science
- 함수
- 반복문
- 알고리즘
- pass by reference
- Deep Learning
- 포인터
- string
- Class
- function
- vscode
- assignment operator
- raw data
- array
- baekjoon
- 배열
- 티스토리챌린지
- programming
- const
- pointer
- 파이썬
- predictive analysis
- OOP
- Python
- 문자열
- 오블완
- C++
- Pre-processing
- 백준
- Today
- Total
Channi Studies
[Data Structure] Heaps - 2 | Heaps Using Arrays 본문
[Data Structure] Heaps - 2 | Heaps Using Arrays
Chan Lee 2025. 5. 8. 03:36Heap Storage
Heaps are typically stored using arrays. Given a tree representation of a heap, the heap's array form is produced by traversing the tree's levels from left to right and top to bottom.
The root node is always the entry at index 0 in the array, the root's left child is entry at index 1, the root's right child is entry at index 2, and so on.

Parents and Child Indices
Because heaps are not implemented with ndoe structures and parent/child pointers, traversing from a node to parent or child nodes requires referring to nodes by index. The table below shows parent and child index formulas for a heap.
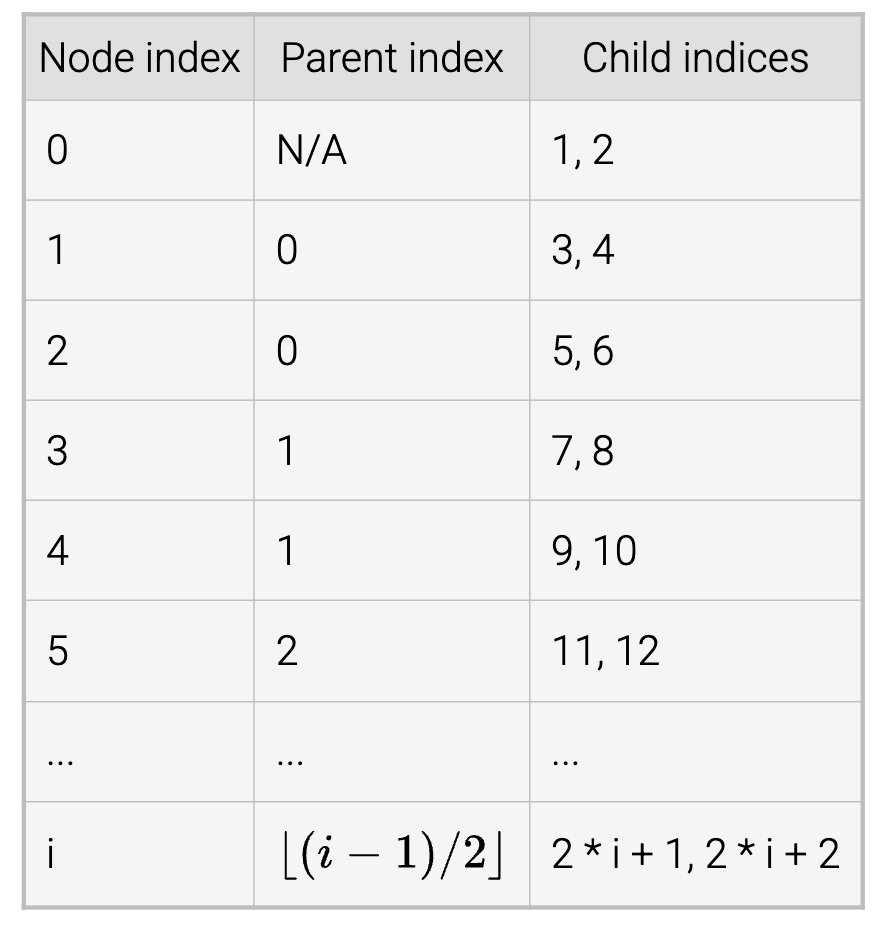
포인터 기반으로 각 노드에 인덱스를 추적할 수 있는 attribute를 추가하는 간단한 방법을 사용할 수 있지만, 그렇다면 수학적으로 계산을 하는 배열 방식보다 비효율적이며 메모리 오버헤드가 발생합니다. 반면 배열로 보관 후 수학적으로 인덱스를 계산 시 모든 자료형이 연속된 메모리 블럭에 존재하므로 캐시 접근성이 매우 뛰어나고 수학적 공식으로 계산하는 것은 포인터 탐색을 피할 수 있기 때문에 훨씬 빠른 시행이 가능합니다.
Percolate Algorithm
Following pseudocode are for array-based percolate-up and percolate-down functions.
MaxHeapPercolateUp(nodeIndex, heapArray) {
while (nodeIndex > 0) {
parentIndex = (nodeIndex - 1) / 2
if (heapArray[nodeIndex] <= heapArray[parentIndex])
return
else {
swap heapArray[nodeIndex] and heapArray[parentIndex]
nodeIndex = parentIndex
}
}
}
MaxHeapPercolateDown(nodeIndex, heapArray, arraySize) {
childIndex = 2 * nodeIndex + 1
value = heapArray[nodeIndex]
while (childIndex < arraySize) {
// Find the max among the node and all the node's children
maxValue = value
maxIndex = -1
for (i = 0; i < 2 && i + childIndex < arraySize; i++) {
if (heapArray[i + childIndex] > maxValue) {
maxValue = heapArray[i + childIndex]
maxIndex = i + childIndex
}
}
if (maxValue == value) {
return
}
else {
swap heapArray[nodeIndex] and heapArray[maxIndex]
nodeIndex = maxIndex
childIndex = 2 * nodeIndex + 1
}
}
}
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] Heap Sort (0) | 2025.05.08 |
|---|---|
| [Data Structure] Heaps Python Implementation (0) | 2025.05.08 |
| [Data Structure] Heaps - 1 | Max-heap (최대 힙) and Min-heap (최소 힙) (0) | 2025.05.08 |
| [Data Structure] Red-Black Tree - 2: Insertion & Balance (0) | 2025.05.02 |
| [Data Structure] Red-Black Tree - 1 (0) | 2025.05.02 |


