| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 배열
- Pre-processing
- Class
- Data Science
- Python
- 알고리즘
- function
- OOP
- 반복문
- pass by reference
- assignment operator
- C++
- vscode
- 함수
- predictive analysis
- pointer
- 포인터
- 문자열
- 백준
- const
- Object Oriented Programming
- programming
- string
- baekjoon
- 티스토리챌린지
- raw data
- array
- Deep Learning
- 오블완
- 파이썬
- Today
- Total
Channi Studies
[Data Structure] Arrays & Linked Lists 본문
[Data Structure] Arrays & Linked Lists
Chan Lee 2025. 3. 10. 05:41Data Structure
A data structure is a way of organizing, storing, and performing operations on data.
Some of the operations that can be performed on a data structure include accessing or updating data, searching for specific data, inserting new data, and removing data.
In our post, we will take on data structures while focusing on the array and linked list.

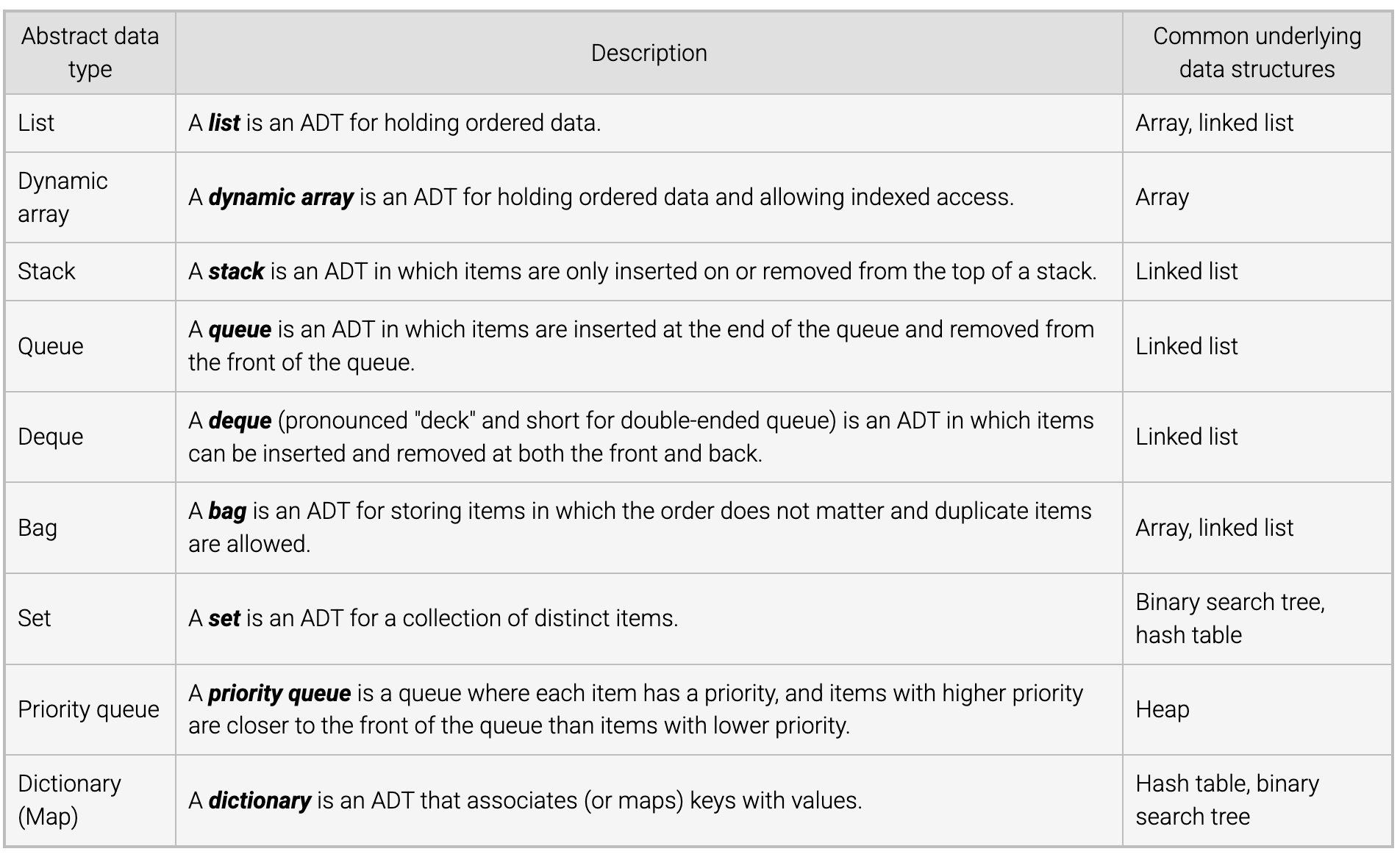
These basic data structures form many abstract data types (ADTs).
These are some common ADTs that has a common underlying data structures from the table above.
Array v.s. Linked List
Both arrays and linked lists store data, but they differ in structure and how elements are accessed.
Array
An array is a data structure that stores a fixed-size collection of elements of the same data type in contiguous memory locations.
Each element in the array is accessed using an index, which represents its position.
Arrays are useful when we need to store multiple values and access them efficiently.
Arrays provide faster access but has a fixed sizes, making insertions and deletions slower.

Structure of an Array
An array is a linear sequence where elements are stored next to each other in memory.
Each element has a unique index, starting from 0.
For example, an array with five numbers:
| Index | 0 | 1 | 2 | 3 | 4 |
| Value | 10 | 20 | 30 | 40 | 50 |
Runtime Complexity: Array (Big O)
1. Accessing Element: O(1)
Since arrays are indexed, accessing an element takes a consistent time, O(1)
2. Insertion: O(n)
Insertion at the end has O(1) complexity.
Insertion at the middle or the beginning has O(n) complexity at worst case, because inserting requires shifting elements.
3. Deletion: O(n)
Removing the last element has O(1) complexity.
Similar to insertion, deletion at the middle or the beginning has O(n) complexity at worst case.
4. Searching: O(log n) or O(n)
Binary serach has O(log n) computational complexity, but it works only for sorted arrays.
Linear search has O(n) time complexity. (For unsorted arrays)
Some real-world applications of arrays: Computer Graphics & Image Processing
Linked List
A linked list is a data structure consists of non-contiguous sequence of nodes scattered in the memory, where each node contains data and a pointer to the next node.
Each node typically contains data, pointer(s).
Elements are not stored sequentially in memory (non-contiguous).
Linked Lists are great for frequent insertions and deletions since elements don’t need to be shifted.

Structure of a Linked List
- Nodes: Each node typically contains:
- Data: The value or payload stored in the node.
- Pointer(s): Have one or two pointers to the next (and previous) node(s).
- Variants:
- Singly Linked List: Unidirectional traversal (simplest), single pointer to the next node
- Doubly Linked List: Traversal in both directions, two pointers to previous/next nodes
- Circular Linked List: The last node’s pointer connects back to first node
Runtime Complexity: Linked List (Big O)
1. Accessing Element: O(n)
O(n) because there is no index in linked lists, so it requires a traversal
2. Insertion: O(1)
At the head: O(1)
At the tail: O(n) without a tail pointer, O(1) with tail pointer
At an arbitrary position: O(n) because it requires traversal
3. Deletion: O(1)
O(1) if you have direct access to the node, and O(n) otherwise since we need to search for it first.
4. Searching: O(n)
When Is One Better?
| Operation | Array | Linked List |
| Access/Search | Fast (O(1) if indexed) | Slow (O(n) since traversal is needed) |
| Insertion | Slow (O(n) if inserting in the middle) | Fast (O(1) at both end) |
| Deletion | Slow (O(n) if removing in the middle) | Fast (O(1) at both end) |
Use an array when fast access to data is desired (e.g. Database indexing, image processing)
Use a linked list when dynamic memory allocation is required, or frequent insertions/deletions occur (e.g. playlists, undo operation)
We will take a look into each data structure later more in detail.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Big-O Notation | 빅 오 표기법 (0) | 2025.03.12 |
|---|---|
| [Algorithm] Growth of Functions and Complexity (0) | 2025.03.12 |
| [Algorithm] Constant Time Operation (0) | 2025.03.12 |
| [Algorithm] Searching: Linear Search & Binary Search (0) | 2025.03.12 |
| Basic Data Structures (0) | 2025.03.05 |




