| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- C++
- 함수
- 배열
- 포인터
- 오블완
- OOP
- const
- pointer
- assignment operator
- 티스토리챌린지
- Data Science
- baekjoon
- 반복문
- pass by reference
- string
- 알고리즘
- Python
- Deep Learning
- 파이썬
- predictive analysis
- Pre-processing
- function
- programming
- Object Oriented Programming
- 백준
- 문자열
- raw data
- array
- Class
- vscode
- Today
- Total
Channi Studies
[Algorithm] Searching: Linear Search & Binary Search 본문
[Algorithm] Searching: Linear Search & Binary Search
Chan Lee 2025. 3. 12. 07:27Searching is a fundamental concept in computer science where the goal is to find the position of a specific item within a dataset.
In this post, we will take a look on a some basic linear search and binary search with the implementation on Python code.
Why do we have to study about searching algorithms?
Searching: Key Concept in Computer Science
- Locate specific item in data
- Fundamental to data interation
Efficient Algorithms:
- Crucial for software performance
- Enhance search speed and resource use (cost-effective solution)
Let's start from linear search.
Linear Search
Linear search, also known as sequential search, starts at the beginning of a list and checks every element for the target value.
The search continues until the element is found or the entire list has been searched.
Time Complexity: O(n)
It means that in the worst-case scenario, the algorithm might have to check every single element, making it inefficient for large datasets.
Ideal for lists that are unsorted or too small to warrant the overhead of more complex algorithms.
A real-world analogy could be flipping through pages of a book one by one to find a specific word.
Python Implementation of Linear Search
A simple python function that takes a list and a target value as arguments, and returns the index of the target if found, or -1 that the target is not in the list.
def binarySearch(arr, target):
low, high = 0, len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return - 1
Binary Search
Binary Search Oveview:
- Requires sorted list
- Compares target to middle element
- Halves search space each step
Efficiency:
- Time complexity: O(log n);
The target is less than any elements in the list (index = 0): log2(n)
The target is larger than any elements in the list (index = len(n) - 1): log2(n) + 1
- Halving reduces comparisons dramatically
Ideal Use Cases:
- Best for large, sorted datasets
- Similar to searching a word in a dictionary
Python Implementation of Binary Search
1. Iterative binary search
def binarySearch(arr, target):
low, high = 0, len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return - 1
2. Recursive binary search
def binarySearchRecursive(arr, target, low=0, high=None):
if high is None: #use default value
high = len(arr) - 1
# Base case: the search space is empty
if low > high:
return -1
# Calculate the middle index
mid = (low + high) // 2
# Check if the middle element is the target
if arr[mid] == target:
return mid
# If the target is smaller than the middle element, search in the left half
elif target < arr[mid]:
return binarySearchRecursive(arr, target, low, mid - 1)
# If the target is larger than the middle element, search in the right half
else:
return binarySearchRecursive(arr, target, mid + 1, high)
Conclusion
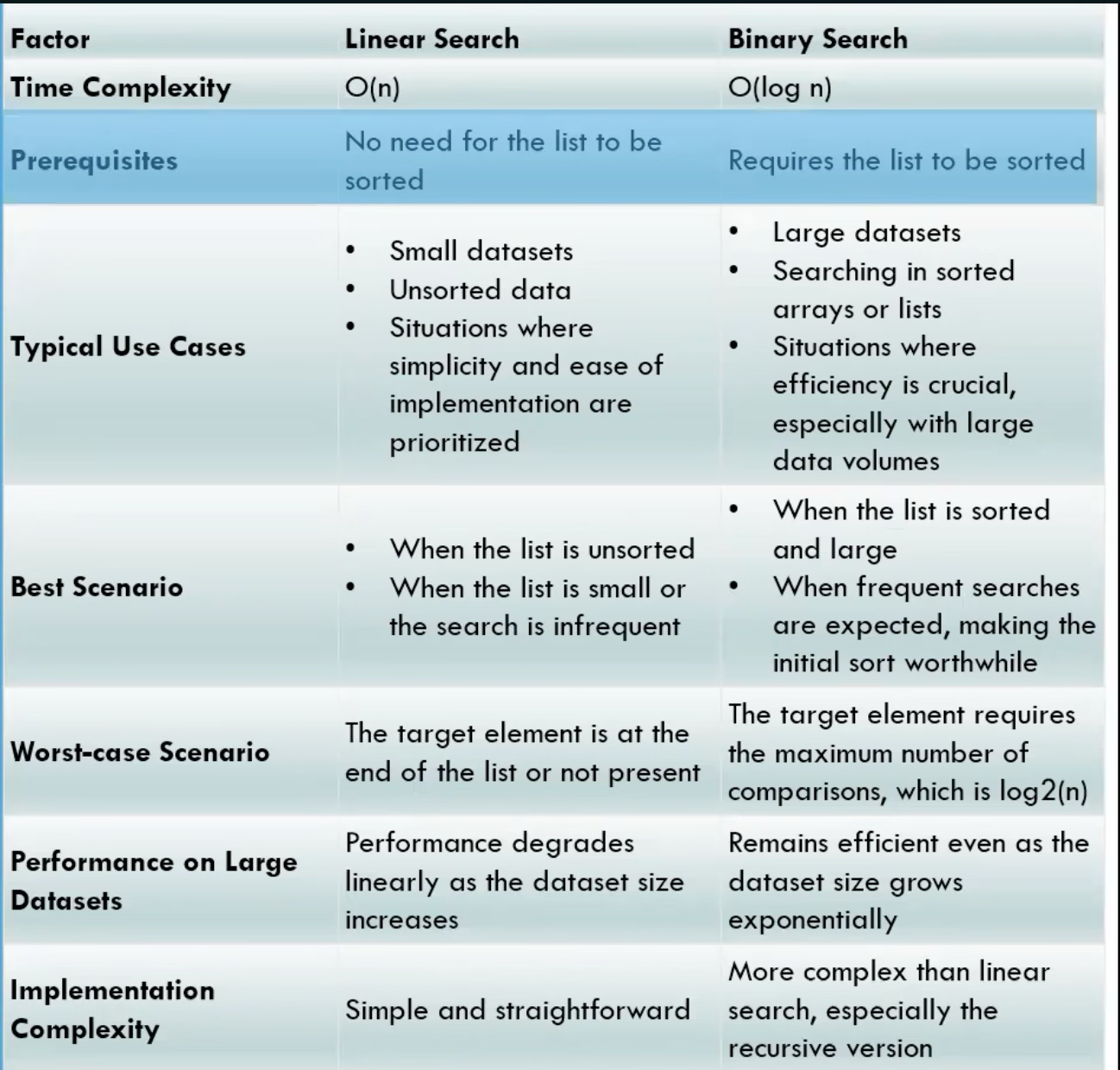
Generally speaking, binary search is a more efficient algorithm when the data set is relatively larger and sorted. However, linear search could still be a good option when we are focusing on small or unsorted data, while focusing on easy and quick implementation. More detailed comparison can be found in the following table:
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Algorithm] Big-O Notation | 빅 오 표기법 (0) | 2025.03.12 |
|---|---|
| [Algorithm] Growth of Functions and Complexity (0) | 2025.03.12 |
| [Algorithm] Constant Time Operation (0) | 2025.03.12 |
| [Data Structure] Arrays & Linked Lists (0) | 2025.03.10 |
| Basic Data Structures (0) | 2025.03.05 |




