| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 반복문
- Python
- array
- OOP
- string
- programming
- 오블완
- 문자열
- pass by reference
- baekjoon
- assignment operator
- function
- 포인터
- raw data
- Pre-processing
- 티스토리챌린지
- 함수
- 파이썬
- C++
- 백준
- Class
- 배열
- predictive analysis
- Data Science
- const
- Object Oriented Programming
- vscode
- pointer
- Deep Learning
- 알고리즘
- Today
- Total
Channi Studies
[Algorithm] Growth of Functions and Complexity 본문
[Algorithm] Growth of Functions and Complexity
Chan Lee 2025. 3. 12. 08:54Upper and lower bounds
An algorithm with runtime complexity: T(N) has a lower bound and an upper bound.
- Lower bound: A function f(N) that is ≤ the best case T(N), for all values of N ≥ 1.
- Upper bound: A function f(N) that is ≥ the worst case T(N), for all values of N ≥ 1.
tip: when considering lower/upper bounds, just consider N = 1
Let's take a look on to an example.
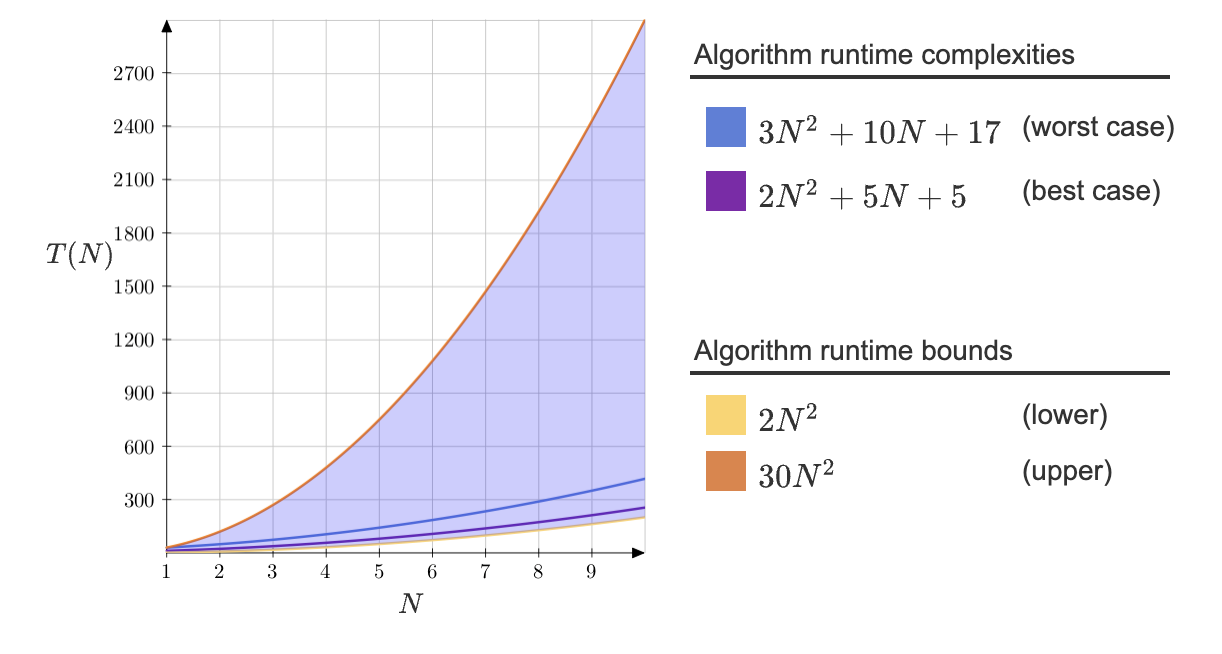
Say that the worst case of time complexity T(N) is 3N^2+10N+17 and the best case is 2N^2+5N+5.
Then, the lower bound should be less than or equal to the best case, giving 2N^2.
The upper bound should be more than or equal to the worst case for all N >= 1.
Then, considering N = 1, 30N^2 is the smallest f(N) such that f(N) >= T(N) for all N >= 1.
There are infinite number of lower and upper bounds, but those were the ways to choose the preferred bounds.
Growth Rates and Asymptotic Notations
Asymptotic notation is the classification of runtime complexity that uses functions that indicate only the growth rate of a bounding function.
Three asymptotic notations are commonly used in complexity analysis:
- O notation provides a growth rate for an algorithm's upper bound.
- Ω notation provides a growth rate for an algorithm's lower bound.
- Θ notation provides a growth rate that is both an upper and lower bound.
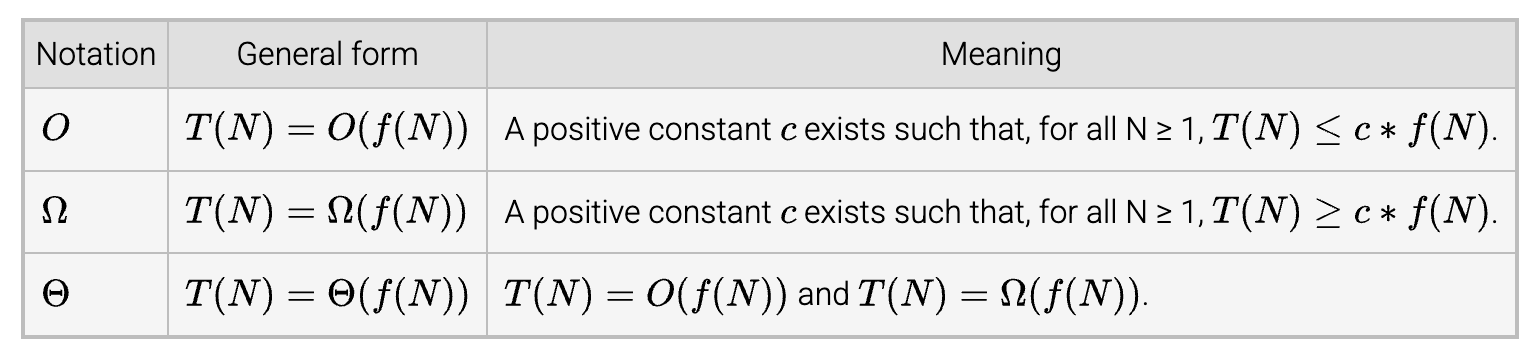
Let's take a look into following example.
Suppose T(N) = 2N^2 + N + 9
Verify whether:
1.) T(N) = O(N^2)
2.) T(N) = Ω(N^2)
3.) T(N) = Θ(N^2)
4.) T(N) = O(N^3)
5.) T(N) = Ω(N^3)
1.): If c = 12, 2N^2 + N + 9 <= 12N^2 ∀N ≥ 1
So It's true
2.): If c = 1, 2N^2 + N + 9 ≥ N^2 ∀N ≥ 1
So It's true
3.): 1 and 2 were true, so it's true
4.): If c = 12, 2N^2 + N + 9 <= 12N^3 ∀N ≥ 1
So It's true
5.) Even if c = 1, 2N^2 + N + 9 <= N^3 starting from N = 4.
So It's NOT true
This post will be followed by a post that delves into the O notation in more details.
'Data Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Sorting] Introduction & Selection Sort (0) | 2025.03.16 |
|---|---|
| [Algorithm] Big-O Notation | 빅 오 표기법 (0) | 2025.03.12 |
| [Algorithm] Constant Time Operation (0) | 2025.03.12 |
| [Algorithm] Searching: Linear Search & Binary Search (0) | 2025.03.12 |
| [Data Structure] Arrays & Linked Lists (0) | 2025.03.10 |




